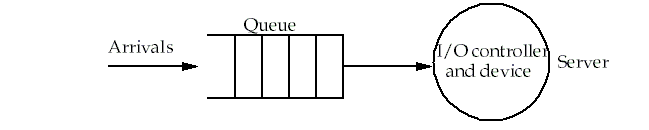
-
Given the important of response time (and throughtput), we need a means of computing values for these metrics.
-
Let's assume our system is in steady-state (input rate = output rate).
-
The contents of our black box.
-
I/O requests "depart" by being completed by the server.
-
Elements of a queuing system:
-
Request & arrival rate
-
This is a single "request for service".
-
The rate at which requests are generated is the
arrival rate
.
-
Server & service rate
-
This is the part of the system that services requests.
-
The rate at which requests are serviced is called the service rate.
-
Queue
-
This is where requests wait between the time they arrive and the time their processing starts in the server.
-
Useful statistics
-
Length
queue
,Time
queue
-
These are the average length of the queue and the average time a request spends waiting in the
queue
.
-
Length
server
,Time
server
-
These are the average number of tasks being serviced and the average time each task spends in the
server
.
-
Note that a server may be able to serve
more than one
request at a time.
-
Time
system
,Length
system
-
This is the average time a request (also called a task) spends in the
system
.
-
It is the sum of the time spent in the queue and the time spent in the server.
-
The length is just the average number of tasks anywhere in the system.
-
Useful statistics
-
Little's Law
-
The
mean number of tasks in the system = arrival rate * mean response time
.
-
This is true only for systems in equilibrium.
-
We must assume any system we study (for this class) is in such a state.
-
This must be between 0 and 1.
-
If it is larger than 1, the queue will grow infinitely long.
-
This is also called
traffic intensity
.
-
Queue discipline
-
This is the order in which requests are delivered to the server.
-
Common orders are FIFO, LIFO, and random.
-
For FIFO, we can figure out how long a request waits in the queue by:
-
The last parameter is the hardest to figure out.
-
We can just use the formula:
-
C is the coefficient of variance, whose derivation is in the book.
-
(don't worry about how to derive it - this isn't a class on queuing theory.)
-
Example: Given:
-
Processor sends 10 disk I/O per second (which are exponentially distributed).
-
Average disk service time is 20 ms.
-
On average, how utilized is the disk?
-
What is the average time spent in the queue?
-
When the service distribution is exponential, we can use a simplified formula for the average time spent waiting in line:
-
What is the average response time for a disk request (including queuing time and disk service time)?
-
Basic assumptions made about problems:
-
System is in equilibrium.
-
Interarrival time (time between two successive requests arriving) is exponentially distributed.
-
Infinite number of requests.
-
Server does not need to delay between servicing requests.
-
No limit to the length of the queue and queue is FIFO.
-
All requests must be completed at some point.
-
This is called an M/G/1 queue
-
M = exponential arrival
-
G = general service distribution (i.e. not exponential)
-
1 = server can serve 1 request at a time
-
It turns out this is a good model for computer science because many
arrival
processes turn out to be
exponential
.
-
Service times
, however, may follow any of a number of distributions.
-
We use these formulas to
predict
the performance of storage subsystems.
-
We also need to measure the performance of real systems to:
-
Collect the values of parameters needed for prediction.
-
To determine if the queuing theory assumptions hold (e.g., to determine if the queueing distribution model used is valid).
-
Benchmarks:
-
Transaction processing
-
The purpose of these benchmarks is to determine how many small (and usually random) requests a system can satisfy in a given period of time.
-
This means the benchmark stresses
I/O rate
(number of disk accesses per second) rather than
data rate
(bytes of data per second).
-
Banks, airlines, and other large customer service organizations are most interested in these systems, as they allow simultaneous updates to little pieces of data from many terminals.
-
TPC-A and TPC-B
-
These are benchmarks designed by the people who do transaction processing.
-
They measure a system's ability to do random updates to small pieces of data on disk.
-
As the number of transactions is increased, so must the
number of requesters
and the
size of the account file
.
-
These restrictions are imposed to ensure that the benchmark really measures disk I/O.
-
They prevent vendors from adding more main memory as a database cache, artificially inflating TPS rates.
-
-
SPEC system-level file server (SFS)
-
This benchmark was designed to evaluate systems running Sun Microsystems network file service, NFS.
-
SPEC system-level file server (SFS)
-
It was synthesized based on measurements of NFS systems to provide a reasonable mix of reads, writes and file operations.
-
Similar to TPC-B, SFS
scales
the size of the file system according to the reported
throughput
, i.e.,
-
It requires that for every 100 NFS operations per second, the size of the disk must be increased by 1 GB.
-
It also limits average
response time
to 50ms.
-
Self-scaling I/O
-
This method of I/O benchmarking uses a program that
automatically scales
several
parameters that govern performance.
-
Number of unique bytes touched.
-
This parameter governs the total size of the data set.
-
By making the value large, the effects of a cache can be counteracted.
-
Self-scaling I/O
-
Percentage of reads.
-
Average I/O request size.
-
This is scalable since some systems may work better with large requests, and some with small.
-
Percentage of sequential requests.
-
The percentage of requests that sequentially follow (address-wise) the prior request.
-
As with request size, some systems are better at sequential and some are better at random requests.
-
Number of processes.
-
This is varied to control concurrent requests, e.g., the number of tasks simultaneously issuing I/O requests.
-
Self-scaling I/O
-
The benchmark first chooses a nominal value for each of the five parameters (based on the system's performance).
-
It then varies each parameter in turn while holding the others at their nominal value.
-
Performance can thus be graphed using any of five axes to show the effects of changing parameters on a system's performance.