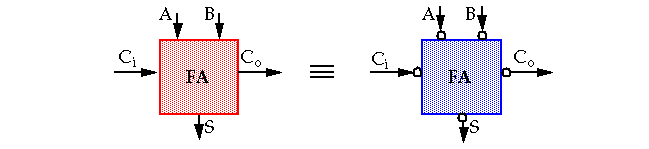-
A simple processor illustrates many of the basic components used in any digital system:
-
Datapath: The core -- all other components are support units that store either the results of the datapath or determine what happens in the next cycle.
-
Memory:
-
A broad range of classes exist determined by the way data is accessed:
-
Read-Only vs. Read-Write
-
Sequential vs. Random access
-
Single-ported vs. Multi-ported access
-
Or by their data retention characteristics:
-
Stay tuned for a more extensive treatment of memories.
-
Control:
-
A FSM (sequential circuit) implemented using random logic, PLAs or memories.
-
Interconnect and Input-Output:
-
Parasitic resistance, capacitance and inductance affect performance of wires both on and off the chip.
-
Growing die size increases the length of the on-chip interconnect, increasing the value of the parasitics.
-
Datapath elements include adders, multipliers, shifters, BFUs, etc.
-
The speed of these elements often dominates the overall system performance so optimization techniques are important.
-
However, as we will see, the task is non-trivial since there are multiple equivalent logic and circuit topologies to choose from, each with adv./disadv. in terms of speed, power and area.
-
Also, optimizations focused at one design level, e.g., sizing transistors, leads to inferior designs.
-
Let's start with addition, since it is very a common datapath element and often a speed-limiting element.
-
Optimizations can be applied at the logic or circuit level.
-
Logic-level optimization try to rearrange the Boolean equations to produce a faster or smaller circuit, e.g. carry look-ahead adder.
-
Circuit-level optimizations manipulate transistor sizes and circuit topology to optimize speed.
-
Let's start with some basic definitions before considering optimizations:
-
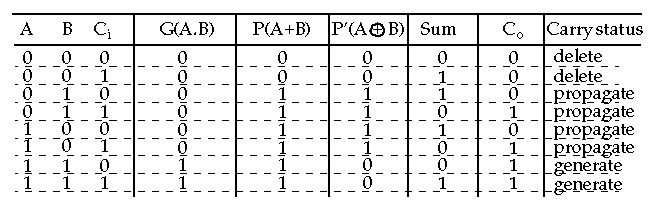
G(A.B)
: (generate)
-
Occurs when a Co is internally generated within the adder (occurs independent of Ci).
-
P(A+B)
: (propagate)
-
Indicates that Ci is
propagated
(passed) to Co.
-
P'(A XOR B)
: (propagate)
-
Used in some adders for the P term since it can be reused to generate the sum term.
-
D(
A
.
B
)
: (delete)
-
Ensures that a carry bit will be deleted at C
o
.
-
The Boolean expressions for S and C
o
are:
-
Sum = A.B.C
i
+ A.B.C
i
+ A.B.C
i
+ A.B.C
i
= A
XOR
B
XOR
C
-
Carry = A.B + A.C
i
+ B.C
i
-
But S and C
o
can be written in terms of G and P':
-
C
o
(G, P') = G + P'C
i
(or P in this case).
-
S(G, P') = P' XOR C
i
-
Note that G and P' are INdependent upon C
i
.
-
(Also, C
o
and S can be expressed in terms of delete (D)).
-
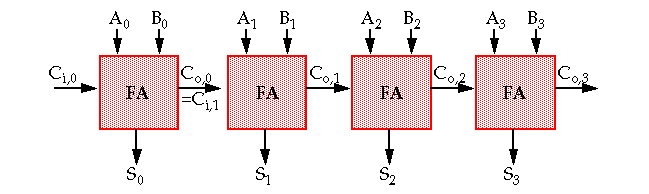
The
critical path
(worst case delay over all possible inputs) is a ripple from
lsb
to
msb
.
-
The delay in this case is proportional to the number of bits, N, in the input words:
-
t
adder
= (N - 1)t
carry
+ t
sum
-
where t
carry
and t
sum
equal the propagation delays from C
i
to C
o
& S.
-
One possible worst case bit pattern (from
lsb
to
msb
) is:
-
Convince yourself that this is true.
-
Note that when optimizing this structure, it is far more important to optimize t
carry
than t
sum
.
-
The inverting property of a full adder can be used to achieve this goal:
-
Thus,
-
S(A, B, Ci) = S(A, B, Ci)
-
Co(A, B, Ci) = Co(A, B, Ci)
-
One possible (un-optimized) implementation:
-
C
o
is reused in the S term as:
-
Sum = A.B.Ci + (A + B + Ci)Co
-
Even with some design tricks, e.g., transistors on the critical path, C
i
, placed closest to the output and symmetrical design, this implementation is slow.
-
The load capacitance in previous version on C
o
consists of 2 diffusion capacitances (inverter) and 6 (next bit) gate capacitances:
-
This version increases Co's load to 4 diffusion caps, 2 internal (sum) gate caps plus the 6 (next bit) gate caps.
-
Serial addition
can be used if area is a concern:
-
In this case, you want equal Sum and Carry delays in order to minimize clock cycle time.
-
Bit-level pipelining
can be used to break the dependency between addition time and the number of bits by inserting FAs between each register bit.
-
Total transistors is 26! Can reduce to 24 by using an inverter for XNOR (see Weste and Eshraghian for an 18 transistor implementation).
-
Note: Sum and Carry delay times are approximately equal.
-
Dynamic Adder Design:
np-CMOS
adder
-
Dynamic Adder Design:
Manchester Carry-Chain
adder.
-
A chain of pass-transistors are used to implement the carry chain.
-
Precharge: All intermediate nodes, e.g. Co,0, charged to VDD.
-
Evaluate: Node Co,k is discharged if there is an incoming carry, Ci,0 and the previous propagate signals are high, P0 to Pk-1.
-
Only 4 diffusion capacitances are present per node but the distributed RC-nature of the chain results in delay that is quadratic with number of bits.
-
Buffers and/or transistor sizing can be used to improve performance.
-
Consider the worst case delay of the carry chain:
-
Elmore delay is given by:
-
The delay of the RC network is then:
-
t
p
= 0.69(C
1
R
1
+ C
2
(R
1
+ R
2
) + C
3
(R
1
+ R
2
+ R
3
) + C
4
(R
1
+ R
2
+ R
3
+ R
4
) +
-
C
5
(R
1
+ R
2
+ R
3
+ R
4
+ R
5
) + C
6
(R
1
+ R
2
+ R
3
+ R
4
+ R
5
+ R
6
)
-
Since R
6
appears
6 times
in the expression, it makes sense to minimize its contribution.
-
Note that reducing R by a factor, e.g.
k
, at each stage increases the capacitance by a factor
k
and increases area.
-
A
k-factor
of 1.5, reduces delay by 40% and increases area by 3.5X.
-
Assume A
k
and B
k
(for k = 1...3) are set such that all P
k
(propagate) are high.
-
In this case, an incoming carry C
i,0
= 1, propagates along the complete chain and C
o,3
= 1.
-
In other words:
-
if (P
0
P
1
P
2
P
3
== 1) then C
o,3
= C
i,0
else either DELETE or GENERATE occurred.
-
Linear Carry-Select
adder:
-
One way around waiting for the incoming carry is to compute the result of
both
possible values in advance and let the incoming carry
select
the correct result.
-
A
Square-Root Carry-Select
Adder (delay = O(N
1/2
)) is constructed by increasing the number of input bits in each block from
lsb
to
msb
.
-
Carry look-ahead
adder (avoiding the ripple altogether):
-
Compute the carries to each stage in parallel.
-
Note that the low-order terms, e.g., P
0
and G
0
, appear in the expression for every bit, making the fanout load large.
-
Carry look-ahead
adder:
-
One possible implementation without using simple logic gates.
-
Size and fan-in of the gates limit the size to about four.
-
The
Logarithmic look-ahead
adder: O(log
2
N) delay:
-
The number of logic levels is proportional to log
2
N, fan-in is limited and the layout is compact (jigsaw puzzle) (see Rabaey for details).
-
Magnitude Comparators
:
-
May be built from an adder, complementer (XOR gates) and a zero detect unit.
-
Think about the modifications necessary to make it a signed comparator (Hint: A couple of XOR gates).
-
Asynchronous: Based on the Toggle register.
-
Not a good choice for performance and testability (with no reset).
-
Replace AND gate with an adder for up/down counting capability.
-
Weste and Eshraghian also show a version that can be initialized.
-
Multiplication can be broken down into two steps:
-
Computation of partial products.
-
Accumulation of the shifted partial products.
-
Multipliers may be classified by the format in which data words are accessed:
-
Serial
-
Serial/parallel
-
Parallel
-
The parallel form computes the partial products in parallel.
-
Parallel Unsigned Multiplication:
-
Parallel Signed Multiplication:
-
Parallel Signed Multiplication:
-
Serial Unsigned Multiplication:
-
Serial/Parallel Unsigned Multiplier shown in Weste and Eshraghian.
-
Right/Left 1-bit shifter: