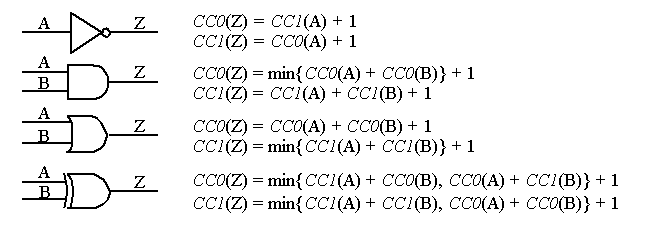Overview

• DFT started with the insertion of test points into the design.

 

• Systematic techniques, such as scan , BIST and boundary scan were developed later.

 

• All are approaches to increase testability by embedding test structures in the CUT.

 

• Testability (one definition by Bennetts '84):
• "A digital IC is testable if test patterns can be generated, applied, and evaluated in such a way as to satisfy predefined levels of performance (e.g., detection, location, application) within a predefined cost budget and time scale"

 

• Cost is key -- it's the reason why semiconductor manufacturers do not do as much testing as is needed to ensure reliable products.

Overview

• Justification for using DFT today:
• Test Generation and Application.
• Deterministic TPG is NP-complete.

 

• What is saved in test generation is offset in test application time.
• Random test pattern generation is low cost but yields long test sets and does not guarantee 100% fault coverage.

 

• Exhaustive test is not feasible.

 

• Characteristics of present VLSI
• Changes in technology have resulted in:
• (a) Smaller, faster devices resulting in a faster operational frequency.
• (b) Higher device density -> more complex designs.
• (c) Lower power supply voltage -> lower noise immunity.
• (d) Thinner and longer interconnect -> increase in crosstalk.
• (e) SOC introduces reuse and new challenges to testing.

Overview

• Characteristics of Present VLSI (cont)
• Higher density and SOC result in larger designs that make test generation more difficult.

 

• Also, accessiblity is more limited, e.g., pin-to-gate ratio is constantly decreasing.

Testability Analysis

• An attempt to quantify testability by Goldstein '79 and Grason '79 resulted in two testability measures, controllability and observability .

 

• Controllability reports the cost of placing a specific value on a node.
• PIs are free (usually assigned a value of 1).
• Output 1 values for AND gates are more expensive than OR gates.

 

• The most popular testability measures are SCOAP; CC0 / CC1 (combinational 0 / 1 -controllability and SC0 / SC1 (sequential 0 / 1 -controllability)

Testability Analysis

• For example:

• In order to calculate controllability , we proceed from inputs to outputs .
• Let's assume the PIs (including branches) are equal to 1.

 

• Initially, all TM values are set to y .
• The entries that remain with y are either uncontrollable or unobservable at the PO.

 

• For nodes F , H and G :
• CC0 (F) = min{ CC0 (A), CC0 (B), CC0 (C)} + 1 = 2
• CC1 (F) = CC1 (A) + CC1 (B) + CC1 (C) + 1 = 4

Testability Analysis

• For nodes F , H and G :
• CC0 (H) = CC1 (A) + CC1 (B) + 1 = 3
• CC1 (H) = min{ CC0 (A), CC0 (B)} + 1 = 2
• CC0 (G) = CC1 (C) + 1 = 2
• CC1 (G) = CC0 (C) + 1 = 2

 

• These are then used to compute the PO controllability:
• CC0 (Y) = CC0 (F) + CC0 (H) + 1 = 6
• CC1 (Y) = min{ CC1 (F), CC1 (H)} + 1 = 3
• CC0 (Z) = CC1 (H) + CC1 (G) + 1 = 5
• CC1 (Z) = min{ CC0 (H), CC0 (G)} + 1 =3

 

• Observability indicates the effort needed to observe the logic value on a node at a PO.
• Assume the cost of observing a PO is 1.

 

• In order to observe values, it is necessary to control the off path inputs.

Testability Analysis

• For example, in order to observe node F on PO Y, it is necessary to control H to 0.
• CO _Y (F) = CO (Y) + CC0 (H) + 1 = 5
• CO _Z (G) = CO (Z) + CC1 (H) + 1 = 4
• CO _Y (H) = CO (Y) + CC0 (F) + 1 = 4
• CO _Z (H) = CO (Z) + CC1 (G) + 1 = 4

 

• We then proceed to the observability measures for the PIs.
• Note that they are observable at either Y or Z .

 

• Consider C via Z:
• CO _Z (C) = CO _Z (G) + 1 = [ CO (Z) + CC1 (H) + 1] + 1 = 5

 

• Consider C via Y:
• CO _Y (C) = CO _Y (F) + CC1 (A) + CC1 (B) + 1 = [ CO (Y) + CC0 (H) + 1] CC1 (A) + CC1 (B) + 1 = 8
• This clearly indicates it is easier to observe C through Z than Y .

Testability Analysis

• Note that the observability numbers for A and B are identical since functions Y and Z are symmetrical in A and B .

 

• Also, sensitizing A and B through G ₁ yeilds the same observability number as C:
• CO _YF (A) = CO _YF (B) = CO _Y (C) = 8.

 

• Note that SA1 faults on the branches of A ₁ and B ₁ (feeding G ₁ ) are not detectable because of the redundancy.
• However, they have finite TMs, comparable to other detectable faults.

 

• Note that both observability and controllability are important:
• An easily controllable node is not necessarily observable.
• The ease of observability is useless unless we can control the node.

Testability Analysis

• Attempts have been made to combine these numbers and correlate them with the ease of test pattern generation.
• This result can then be compared, for example, with the total number of tests that detect each fault (in the exhaustive sense).

 

• TMs can be generated quickly (unlike test generation), in O(n) time.
• They are used to aid ATPG algorithms suce as FAN and SOCRATES.

 

• They are also used to determine test insertion points to facilitate controllability and observability for built-in self-test (BIST).

 

• Ad hoc strategies (before DFT came along) include:
• Initializing a sequential circuit before testing it.
• Adding control and observe points to increase testability.
• Dividing the circuit into smaller partitions.

 

• Although initializing a circuit is not required for proper operation, it is needed in order to test it.

Initialization and Test Point Insertion

• However, such sequences may be long and costly to develop.
• Also, not every sequential circuit has a synchronzing or homing sequence.

 

• It is obvious that increasing the number of observation points facilitates testing.

• Add an observation point, OP , if node P is difficult to observe through U .

Test Point Insertion

• We noted earlier that A and B have undectable SA1 faults in this circuit:

• Leaving these undetected can result in unpredictable behavior.

 

• Control Points :

Test Point Insertion

• Note that the controllability of all node of U are affected by the insertion of the control points, as are the observabilities of all nodes that go through P.

 

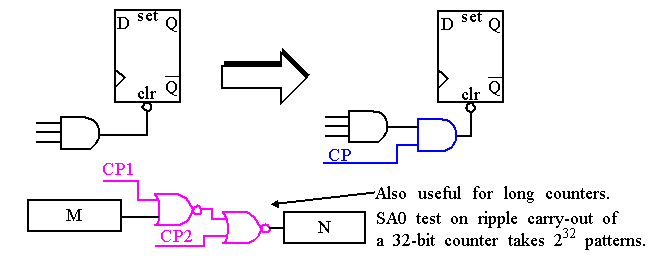
• Thus, CP1 and CP2 ease control of P and affect observability of subcircuit W .
• These add constraints, e.g. to observe, CP1 and CP2 must be low.

 

• Test point insertion is actually more valuable in sequential circuits .
• It is difficult to reset some storage devices because of complex logic.

Test Point Insertion

• Here, M and N can be tested independently.

 

• Also, modular counters should be used when possible.
• For example, replace a Mod 24 counter with a Mod 3 and Mod 8 counter.

 

• This reduces the test length from 2 ²⁴ to 2 ⁸ .

 

• We will soon discuss the ultimate for test point insertion for sequential logic ( scan path ).

 

• BIST can make effective use of test point insertion also.
• Random pattern resistive ( RPR ) faults are faults not easily detectable by Pseudo-Random (PR) patterns.

 

• Control points can be added in troublesome regions, that are treated as PIs by the BIST circuitry.