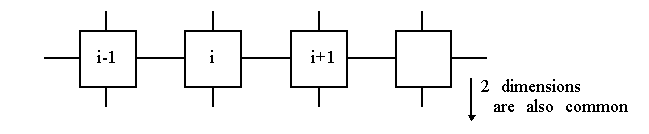-
As we noted, testability measures of a circuit are a function of its
depth
.
-
Smaller circuits are easier to test.
-
If large circuits can be broken down into smaller subcircuits, it is possible to add
OP
and
CP
points.
-
Hardware is needed to partition a circuit.
-
Generally, this is done with MUXs.
-
MUXs can be used to
isolate
each segment and improve the TMs.
-
The MUXs are
transparent
during normal operation.
-
Here, the inputs provided by G
2
become
control points
instead.
-
Also, the outputs of G
1
to G
2
are diverted to improve
observability
.
-
Two
2-to-1
MUXs allow the b partition to be directly
observable
on Z
2
(
S
=0) or the a and g partitions to be
controlled
to Z
1
and Z
2
(
S
=1).
-
In the latter case,
I
is used to control the "off-path" input.
-
It is also possible to do the segmentation by
sensitization of the test data
.
-
This is based on the
pseudo-exhaustive
method proposed by McCluskey.
-
Sensitized Partitioning:
-
An
N
-input circuit is partitioned into
M
segments, each of which has K
i
PIs (with K
i
<
N
).
-
Testing all partitions exhaustively requires:
-
Our earlier analysis of the previous circuit required
4
patterns to test a with the OR gate controlled to a 0.
-
The total test length was determined to be
20
(4 + 8 + 8).
-
However, its possible to
compact
the test set to 16.
-
For example, patterns for a that result in
R
=0 can be combined with patterns for b that make
W
=0.
-
Additional reductions may be possible by considering
don't cares
.
-
Verification testing
is applicable when each output is a function of only a subset of PIs.
-
The three outputs depend on 3, 3, and 2 PIs.
-
An exhaustive test is
32
patterns. Each output requires 8, 8, and 4 =
20
.
-
McCluskey has shown that if 2 inputs
never
appear in the same output function, the
same
test signal can be applied to both.
-
The scheme is called
Maximum Test Concurrency
(
MTC
), and it reduces the number of tests.
-
The method requires an
m
X
n
dependency matrix (
m
is number of POs):
|
|
a
|
b
|
c
|
d
|
e
|
|
f
|
1
|
1
|
1
|
0
|
0
|
|
g
|
0
|
1
|
1
|
1
|
0
|
|
h
|
0
|
0
|
0
|
1
|
1
|
-
A 1 is present when the output function depends on an PI.
-
Next we partition the matrix such that
no more than one PI
affects the same PO.
-
For example, no partition has more than one 1 in a row.
|
|
a
|
d
|
b
|
c
|
e
|
|
f
|
1
|
0
|
1
|
1
|
0
|
|
g
|
0
|
1
|
1
|
1
|
0
|
|
h
|
0
|
1
|
0
|
0
|
1
|
-
This partitioning is not unique, we could have combined
b
and
e
, or
a
and
e
. The partitioning problem is
NP-complete
.
-
The information in the partition matrix determines the total number of test patterns, 2
K
where
K
is the maximum number of 1's in a row.
-
This is called the
maximum dependency
.
-
K
= 3 in this case, which implies 2
3
patterns are required for pseudoexhaustive test! (75% saving over exhaustive).
-
Note, that variables in the same partition can assume the same values in the test, e.g. columns
a
-
d
and
c
-
e
.
|
a
|
b
|
c
|
d
|
e
|
|
0
|
0
|
0
|
0
|
0
|
|
0
|
0
|
1
|
0
|
1
|
|
0
|
1
|
0
|
0
|
0
|
|
0
|
1
|
1
|
0
|
1
|
|
1
|
0
|
0
|
1
|
0
|
|
1
|
0
|
1
|
1
|
1
|
|
1
|
1
|
0
|
1
|
0
|
|
1
|
1
|
1
|
1
|
1
|
-
Here, we determined exhaustive is
256
patterns, and
96
for exhaustive test sets for the partitions.
-
The dependency matrix and compaction using
A
and
F
give 2
6
=
64
patterns:
|
|
A
|
B
|
C
|
D
|
E
|
F
|
G
|
H
|
|
A
|
F
|
B
|
G
|
C
|
D
|
E
|
H
|
|
Z1
|
1
|
1
|
1
|
1
|
1
|
0
|
0
|
0
|
|
1
|
0
|
1
|
0
|
1
|
1
|
1
|
0
|
|
Z2
|
0
|
0
|
1
|
1
|
1
|
1
|
1
|
1
|
|
0
|
1
|
0
|
1
|
1
|
1
|
1
|
1
|
-
There are
6
different partitioning,
A
and
B
combined with
F
,
G
and
H
.
-
Regularly structured circuits are arrays of identical cells.
-
RAMs
,
FPGAs
,
array multipliers
and other circuits that are deliberately designed in a modular fashion to facilitate layout.
-
Combinational regular structures are called
Iterative Logic Arrays
(
ILA
s).
-
Some of these structures are easily testable with a
constant
number of test patterns, independent of the size of the circuit!
-
The term
C-testable
(Friedman) is used in these cases.
-
Sometimes it's possible to redesign the circuit to make it C-testable, e.g., array multipliers.
-
Consider the
1-D
array of adders:
-
As noted, 8 patterns represent an exhaustive test.
-
An n-input parity tree is testable with only 4 patterns (00, 01, 10, 11):
-
The parity tree is a fan-out free circuit, therefore we need only detect
SA
faults on the PIs.
-
R
and
S
label the sequence of exhaustive patterns applied to the inputs of G
1
.
-
G
1
produces sequence
T
, combined with
R
yields an exhaustive test.
-
The three vectors have the property:
 where V
where V
i
, V
j
and V
k
are any combination of
R
,
S
and
T
.