Overview

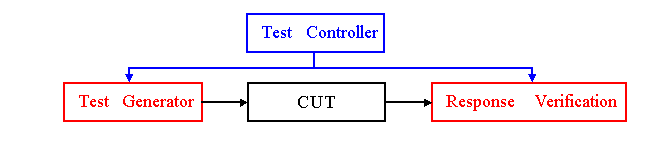
• Benefits of BIST:
• As a means of dealing with the cost of TPG.
• As a means of dealing with increasingly larger volumes of test data.
• As a means of performing at-speed test.

 

• BIST entails three tasks:
• TPG
• Test application
• Response verification

 

• Types of BIST:
• Memory BIST
• Logic BIST
• Combinations for testing RAM-based FPGAs.

 

• We will focus on logic BIST , used for testing random logic.

Overview

• Logic BIST uses pseudorandom ( PR ) tests, generated using a Linear Feedback Shift Register ( LFSR ) or cellular automata.

 

• Usually much longer than deterministic tests but much less costly to generate.

 

• The large volume of data usually requires some sort of compactor to compress the responses.
• There are several types but signature analyzers are the most popular.

• All components are on-chip.

 

• The controller manages the application of the test.

PseudoRandom TPG and LFSRs

• PseudoRandom ( PR ) implies random patterns without repetition .

 

• We've already seen an example of an LFSR used to generate PR patterns.

LFSRs

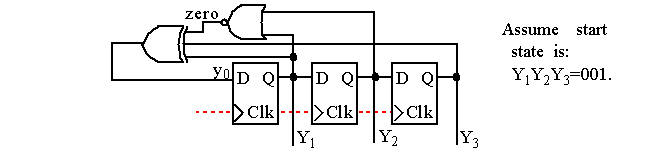
• For (a), the parity of the feedback tabs defines the input, Y ₀ .

• Let y ₀ y ₁ y ₂ represent the present state of the registers and Y ₁ Y ₂ Y ₃ represent the next state , then Y ₁ = y ₀ , Y ₂ = y ₁ and Y ₃ = y ₂ .

Clk	y0	Y1	Y2	Y3		Clk	y0	Y1	Y2	Y3		Clk	y0	Y1	Y2	Y3
	1	0	0	1			1	0	0	1			1	0	0	1
1	1	1	0	0		1	0	1	0	0		1	1	1	0	0
2	1	1	1	0		2	0	0	1	0		2	0	1	1	0
3	0	1	1	1		3	1	0	0	1		3	0	0	1	1
4	1	0	1	1								4	1	0	0	1
5	0	1	0	1
6	0	0	1	0
7	1	0	0	1

• The leftmost (a) LFSR was arbitrarily initialized to 001 .
• Generating 000 is not possible (the last row is identical to the first row).
• The maximal cycle of the LFSR is 7: (2 ³ - 1).

LFSRs

• Note that the relationship between the maximal cycle and the # of feedback tabs is not linear.
• Example (c) has 3 feedback tabs but can only generate 4 patterns.
• Adding a NOR as shown allows the all-zero pattern.

Clk	y0	zero	Y1	Y2	Y3
1	1	1	0	0	0
2	1	0	1	0	0
3	1	0	1	1	0
4	0	0	1	1	1
5	1	0	0	1	1
6	0	0	1	0	1
7	0	0	0	1	0
8	0	1	0	0	1

LFSR Configurations

• Two configurations:

• Note, there is only a tap and an XOR gate if C _i =1.

LFSR Configuration Examples

• This LFSR is equivalent to the version given in (a) previously.

 

• LFSRs that implements polynomial 1 + X ³ + X ⁴ .

Analytical Framework for LFSRs

• The truth table for the XOR gate indicates it performs addition and subtraction , modulo 2.

a	b	a XOR b	a+b (sum)	a-b (diff)	a+b (carry)	a-b (borrow)
0	0	0	0	0	0	0
0	1	1	1	1	0	1
1	0	1	1	1	0	0
1	1	0	0	0	1	0

• Note that carry and borrow are not implemented because of the modulo 2.

 

• Expressing the output, Y _j , as a function of time:

• As a function of Y ₀ , using X ^j as a translation operator:

Analytical Framework for LFSRs

• In the standard form, Y ₀ is the sum of other states as given by:

 

• Substituting:

Analytical Framework for LFSRs

• Assuming

• where

 

• The characteristic polynomials for (a), (b) and (c) given earlier are:
• C ₁ =1, C ₂ =0, and C ₃ =1 yields P ₃ (X) = 1 + X + X ³
• C ₁ =0, C ₂ =0, and C ₃ =1 yields P ₃ (X) = 1 + X ³
• C ₁ =1, C ₂ =1, and C ₃ =1 yields P ₃ (X) = 1 +X +X ² + X ³

 

• The length of the LFSR sequence is determined by its characteristic polynomial.
• Only a primitive polynomial guarantees a maximal-length sequence of 2 ^N - 1.

Operations on Polynomials

• Multiplication uses modulo 2 addition, e.g., x ⁱ + x ⁱ = 0.
• Division will be useful in response compaction.

• Irreducible polynomial properties :
• Cannot be factored, is divisible only by itself and 1, has a odd number of terms (including 1), is primitive if smallest k even divisible into 1 + x ^k is k = 2 ^N -1 (with N the degree of the polynomial).

Primitive Polynomials

• All polynomials of degree 3 that include the 1 term:

• (b) and (c) are primitive, e.g., they divide evenly into x ⁷ - 1.
• (a) and (d) are reducible, e.g., x ³ + 1 = (x + 1)(x ² + x + 1).

 

• Text lists primitive polynomials up to N=48, all of which include the terms 1 and X ^N and require at most 3 XORs (fewer is better, of course).

 

• The configuration of the LFSR introduces autocorrelation between consecutive sequences, e.g.,Y ₂ and Y ₃ from slide 4 give:
• 001110
• 100111
• This makes it difficult to detect some faults ( Random Pattern Resistant ( RPR )).

Response Compaction

• The response of the logic under test needs to be checked after test application with an LFSR.

 

• It is difficult to check the response of every pattern (storage requirements).
• Instead, the responses are compressed and the compressed response is checked.

 

• The type of compression used here typically losses information and allows aliasing (identical faulty and fault-free circuit responses).
• The probability of aliasing decreases as the length of the test increases .

 

• There are several compaction testing techniques:
• Parity testing
• One counting
• Transition counting
• Syndrome calculation
• Signature analysis

Parity and One Counting

• Parity testing : simplest but most lossy.

• Detects all single bit errors and multiple bit errors of odd cardinality.

 

 

• One Counting : # of 1's in the response stream is compared with fault free value.

• The counter counts up by 1 each time a response, r _i , is 1.
• Under exhaustive test, the # of 1's represents the # of minterms in a fault free circuit ( syndrome testing : a special case of 1's counting).

One Counting

• Consider the following exhaustive test:

• For the fault-free circuit, the 1-count is 5.
• The faults a/0 and a/1 would be detected since the counts would be 4 and 6.

 

• An upper bound on the probability of aliasing, given a test of length L (with 2 ^L - 1 strings) and a fault-free 1-count of m is:

• C( L , m ) - 1 represents the number of L bit strings with m 1's that are aliases.

 

• Note that C( L , m ) is symmetrical but not uniform and has a peak at L /2.
• Therefore, the probability is smaller for small and large values of m .

One Counting

• For the circuit shown above, P _alias is 55/255 ~= 0.2.
• However, in this case, the test does not cause ANY aliasing.
• Are all of the 255 strings of length 8 possible?
• How many faults are possible?

 

• The non-uniform probability is accounted for by considering the probability that the fault-free circuit produces m 1's

 

• Consider the pseudoexhaustive test:

• Fault-free circuit 1-count is 3 and L is 5, which gives P _alias 10/31 ~= 0.3.
• Aliasing occurs only for 1 fault, a/1 , but its not detected anyway.

Transition Counting and Signature Analysis

• Transition Counting : Only the number of transitions ( 0->1 and 1->0 ) are counted in this compaction scheme.

 

• The signature is given by:

 

• Signature Analysis ( cyclic redundancy checking ): Most popular technique.
• The compactor is an LFSR which takes the response string, M(t) as input.

 

• An N -bit signature is stored in the N -bit LFSR after the application of the L test patterns ( L -> N compaction).

Signature Analysis

• The signature is just the remainder of the division of the response by the characteristic polynomial of the LFSR, P(X).
• For example, assume M(t) = { 10110001 } is applied to either in state ( 000 ):

T	M(t)	y0	y1	y2	y3	M(t)	y0	y1	y2	y3
0	1	1	0	0	0	1	1	0	0	0
1	0	0	1	0	0	0	0	1	0	0
2	1	0	0	1	0	1	1	0	1	0
3	1	0	0	0	1	1	0	0	0	1
4	0	0	0	0	0	0	0	0	0	0
5	0	0	0	0	0	0	0	0	0	0
6	0	0	0	0	0	0	0	0	0	0
7	1	1	0	0	0	1	1	1	0	0
8	x	X	1	0	0	x	x	1	0	0

Signature Analysis

• The signatures, X ² , are the result of the division of M(X) (a representation of M(t)) by the characteristic polynomials of the LFSRs.
• M(X) = P(X)Q(X) + R(X).

 

• With M(t) = { 10110001 }, M(X) = X ⁷ + X ⁵ + X ⁴ + 1.

Fault Detection using Signature Analysis

• Assume we have a CUT and a test set of length L , such that at least one pattern detects each fault, f , in the CUT.

 

• The response is applied to the N -stage signature analyzer implementing characteristic polynomial, P(X).

 

• The fault is detected if the fault signature S _f is different from the fault-free signature S:

• The signature, S, is the remainder
• Therefore, aliasing (masking) occurs when R _f (X) = R(X).

• Since the polynomial has a finite number of remainders, it is not possible to eliminate aliasing unless the L <= N .

Aliasing Probability using Signature Analysis

• Assume the response of a CUT is L bits long.

 

• The structure of the LFSR distributes the signatures of all possible response streams (strings) of length L (2 ^L ) evenly over all possible signatures.
• For an N -stage LFSR, the #, N _s , of strings/signature is:

• For a particular fault-free response, there are 2 ^L-N -1 erroneous strings that produce the same signature.

 

• Given there are 2 ^L -1 possible erroneous strings, the aliasing probability is:

Aliasing Probability using Signature Analysis

• This is a strange result since it is independent of the polynomial.

 

• This suggests that the P(X) = X ^N , which is just a shift register whose "remainder" is the last N bits of the test response, works equally well!

 

• For example, a 16-bit LFSR may detect (1 - 2 ^-16 ) = 99.9984% of the error responses.
• However, since there is no direct correlation between faults and error masking, this is not necessarily the same percentage of faults detected.

 

• Also, this assumes that the number of faulty response streams is 2 ^L - 1 and that each faulty response is equally likely.
• Neither of these is true in general.

 

• Several schemes have been proposed that minimize aliasing, e.g., reversing the test sequence, using multiple MISRs, taking multiple signatures.
• All require extra hardware or increased test time.