Multiple Scan Chains

• Test application time is a function of the number of FFs scanned.

 

• Test time is reduced if more than one chain is operated in parallel .

 

• This is particularly effective for BIST design, because the pseudo-random tests sets are extremely long.

 

• Also, since some circuits use multiple clocks to control different parts of the circuit, it is easier to add scan to the different sections separately.

 

• For external applied tests (not BIST), multiple chains require more than one pin, unless they are multiplexed with several PIs.

 

• Multiple chains pose other challenges such as balancing the number of elements in each chain, while minimizing interconnect length.

Cost/Benefits of Scan

• Complexity/area is increased through the use of scan FFs.
• Scan FF area overhead is usually reasonable since the fraction of FFs per combinational logic is small.

 

• The most significant overhead is in routing .
• Research has has focused on scan ordering heuristics that minimize the area of the extra interconnect.

 

• Additional I/Os needed.
• For LSSD, SI, SO, SE, f ₂ and f ₃ are needed.

 

• SI and SO may be multiplexed with a PI and a PO.

 

• Test time per pattern is increased (due to the serial nature of scan).

Cost/Benefits of Scan

• Scan can degrade performance.
• MUX scan clearly adds delay.

 

• Two-port FFs or latches minimize the additional delay, as indicated previously.

 

• Test generation costs can be significantly reduced, which can also lead to higher fault coverage.

 

• Increased power dissipation under "At-Speed" testing.
• External scan is applied at a slower rate than the operating frequency.

 

• Scan combined with BIST, however, is often run at-speed, and the heat generated by clocking all FFs simultaneously can be excessive.

 

• Some designs are not ameanable to scan.

Partial Scan

• In order to reduce some of the penalties associated with full scan, only a subset of the FFs need to be made scannable.

 

• Note that the circuit in this case remains sequential and sequential test methods are still required.

 

• The main trade-off is between the number and identify of the FF s to make scannable and fault coverage , where the "best" strategy is defined by:
• One that requires the minimal effort for sequential ATPG.
• One that minimizes area overhead.
• One that minimizes interconnect.
• One that minimizes additional delays.

 

• Easing test pattern generation seems to be the most important factor.

 

• The complexity of sequential ATPG is a function of the number of FFs in feedback loops or the number of FFs between two scanned FFs.

Partial Scan

• Strategies for the selection of the appropriate FFs to make scannable are based on:
• Testability analysis .
• Usually not useful by itself since TMs are not necessarily good predictors of TPG difficulty.
• Structural analysis .
• Test pattern generation .

 

• One strategy to determine the value of making a FF scannable is to compute the fault covereage after making just that FF scannable.
• This yields the best results but is computationally expensive.

 

• A feasible strategy is to combine TMs with the second two strategies.

 

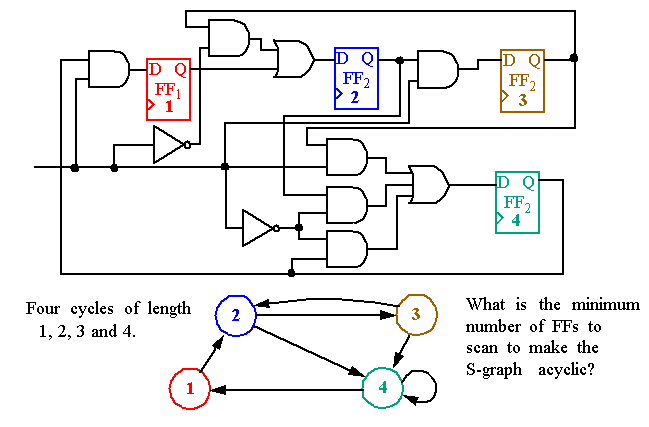
• Structural analysis creates a directed graph model of the CUT.
• Here, the FF are the vertices and the combinational logic gates are the edges between the FFs.

Structural Analysis of Partial Scan

• A cyclic graph S is represented as G(V, E) where vertex, v _i , represents a FF and edge (v _i , v _j ) is a connection between the output of one FF and the input of another.

 

• A path is a sequence of edges from v _i and v _n .

 

• The sequential depth of a circuit is the longest cycle in the circuit.
• Circuits with larger sequential depths increase the difficulty of TPG.

 

• Starting with a graph, the idea is to select the minimum # of FF s that change the graph into an acyclic graph.

 

• The minimum # of FFs is called the Minimal Feedback Vertex Set ( MFVS ).

 

• Under these conditions, it is possible to use a combinational ATPG with minor changes.

 

• Determining the MFVS is NP-complete and therefore, heuristics are used.

Structural Analysis of Partial Scan

• For example

Structural Analysis of Partial Scan

• The adjacency matrix is given as:

	FF1	FF2	FF3	FF4	Tot	FF1	FF2	FF3	FF4	Tot
FF1	0	1	0	0	1	0	1	0	0	1
FF2	0	0	1	1	2	0	0	1	1	2
FF3	0	1	0	1	2	0	1	0	1	2
FF4	1	0	0	1	2	0	0	0	0	0
Tot	1	2	1	3		0	2	1	2

• Element a _ij is 1 if FF i feeds FF j .

 

• One heuristic to determine how to break the cycles is to sum the indegrees and outdegrees .
• This provides a measure of the # of possible loops through the vertex.

 

• Here, FF4 has the largest estimate, 5, followed by FF2 with 4.
• Scanning FF4 breaks all loops except FF2 - FF3 of depth 2.

 

• For an acyclic graph, scan FF2 or FF3 .
• Proximity information may be used to determine other choices.

Test Application under Partial Scan

• Consider the one clock MUX version of scan.

 

• After test application, the system is clocked once to latch the response.

 

• During scan out, all FFs are clocked and the non-scanned FFs will latch new values changing the circuit state.

 

• In order to retain the non-scan FF state after test application, one can:
• Use separate clocks for the scan and non-scan FFs.
• Add a hold mode to the non-scan FFs.

• Scan-set can also be used, with no special provisions for partial scan.

Ordering Scan Chain FFs

• The order of the FFs affects two of the cost measures, interconnect length and test application time .

 

• This is usually done after synthesis with the netlist, before place and route.
• It is also possible to place and then find the best way to "stitch" them together.

 

• Note the optimal strategy for test application is often in contradiction with the optimal routing strategy.

 

• Multiple chains is the best means of dealing with this, but costs extra pins or multiplexers.

 

• In datapath circuits, registers are often used as input or output only .
• Scheduling multiple test sessions can be an advantage since it minimizes test application time.

Ordering Scan Chain FFs

• For example, data path with 20 FF s:

• Assume it's possible to merge the two tests for a total of 300 test vectors.
• The total number of clocks is 300*(20 + 1) + 20 = 6320 .
• (+1 is used to latch the internal values).

 

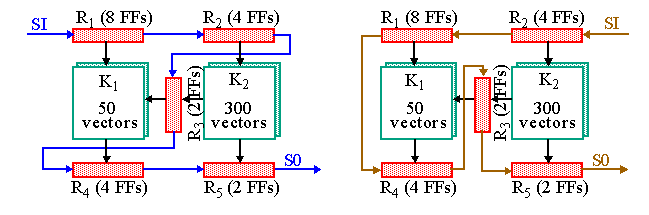
• However, R ₁ and R ₂ are drivers for K ₁ and K ₂ , R ₄ and R ₅ are recievers while R ₃ is a driver/receiver.

 

• Let's analyze the left configuration.

Ordering Scan Chain FFs

• Example (cont).
• The first 50 (common) patterns are shifted into the 14 FFs of R ₁ , R ₂ and R ₃ while the results of the previous pattern is shifted out of R ₃ -> R ₅ .

 

• Test time for this portion is 50(14 + 1) = 750 cycles.

 

• The remaining 250 patterns are to be applied through R ₂ , which requires 12 cycles for each pattern.
• Again, the results of the previous patterns are scanned out of R ₃ and R ₅ .

 

• Test time for this portion is 250(12 + 1) = 3250 cycles.

 

• Total test time is 750 + 3250 + 8 = 4008 , a 37% reduction in time with a corresponding heat dissipation benefit.

 

• The right configuration gives 50(18 + 1) and 250(4+1) + 4 = 2204 cycles.
• An improvement of 45% over previous and a 65% over original.

Optimizing Interconnect Wiring

• It is important to minimize interconnect length , particularly with interconnect delay on order with gate delays and large interconnect chip areas.

 

• Determining FF order can NOT be done only at the logic level.
• It must be considered at the physical layer as well.

 

• In addition to the serial FF connections, other wires to minimize include SE the Clk .

 

• Note that the cost function consists of both interconnect wire lengths and ordering constraints to minimize test application time, as given above.

 

• At the physical level (after placement), the problem can be modeled as finding the shortest route such that each FF is visited once and only once.

 

• Let's use graph theory to find a solution.

Optimizing Interconnect Wiring

• Let G( V , E , W ) represent the CUT where:
• represents a FF.

• is a connection from v
_i to v _j .

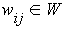• is the length of the edge (v
_i , v _j ).

 

• The elements of the adjacency matrix are the weights w _ij .

 

• Krusal's greedy algorithm is used to find the minimal spanning tree .
• Here we start with the smallest weight , w _ij , which connects v _i and v _j .
• Vertices v _i and v _j are removed.
• The smallest weighted edge from v _i or v _j to v _k is added.
• Repeat the process using v _i and v _k until all vertices are visited.

 

• Note that the algorithm starts with a matrix in which all distances between FFs has been computed in advance (n ² distances).
• Heuristics (e.g. neighborhoods ) can be used to reduce the # of elements.