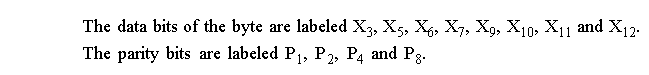-
The processor can usually address a memory space that is
much larger
than the memory space covered by an individual memory chip.
-
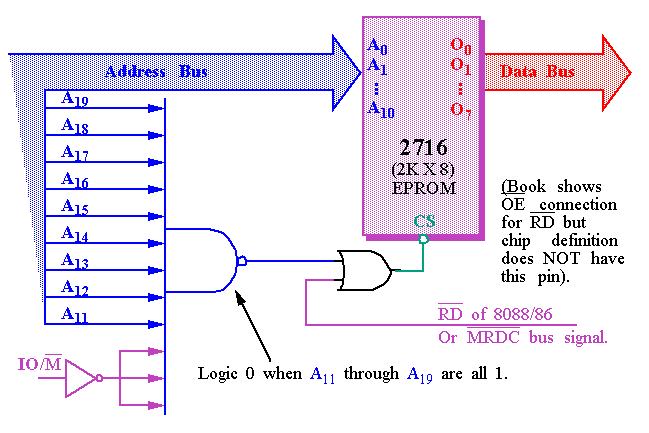
In order to splice a memory device into the address space of the processor, decoding is necessary.
-
For example, the 8088 issues
20-bit
addresses for a total of
1MB
of memory address space.
-
However, the BIOS on a 2716 EPROM has only 2KB of memory and
11
address pins.
-
A decoder can be used to decode the additional
9
address pins and allow the EPROM to be placed in
any
2KB section of the 1MB address space.
-
To determine the address range that a device is mapped into:
-
This 2KB memory segment maps into the
reset location
of the 8086/8088 (FFFF0H).
-
NAND gate decoders are not often used.
-
Rather the 3-to-8 Line Decoder (74LS138) is more common.
-
The 3-to-8 Line Decoder (74LS138)
-
Note that all
three
Enables (G2A, G2B, and G1) must be active, e.g. low, low and high, respectively.
-
Each output of the decoder can be attached to an 2764 EPROM (
8K X 8
).
-
The EPROMs cover a 64KB section of memory.
-
Yet a third possibility is a
PLD
(Programmable Logic Device).
-
PLDs come in three varieties:
-
PLA
(Programmable Logic Array)
-
PAL
(Programmable Array Logic)
-
GAL
(Gated Array Logic)
-
PLDs have been around since the mid-1970s but have only recently appeared in memory systems (PALs have replaced PROM address decoders).
-
PALs and PLAs are
fuse-programmed
(like the PROM).
-
Some are erasable (like the EPROM).
-
A PAL example (16L8) is shown in the text and is commonly used to decode the memory address, particularly for 32-bit addresses generated by the 80386DX and above.
-
AMD 16L8 PAL decoder.
-
It has 10 fixed inputs (Pins 1-9, 11), two fixed outputs (Pins 12 and 19) and 6 pins that can be either (Pins 13-18).
-
AND/NOR device with logic expressions (outputs) with up to 16 ANDed inputs and 7 ORed product terms.
-
The memory systems "sees" the 8088 as a device with:
-
20
address connections (A19 to A0).
-
8
data bus connections (AD7 to AD0).
-
3
control signals, IO/M, RD, and WR.
-
We'll look at interfacing the 8088 with:
-
32K
of EPROM (at addresses F8000H through FFFFFH).
-
512K
of SRAM (at addresses 00000H through 7FFFFH).
-
The EPROM interface uses a 74LS138 (3-to-8 line decoder) plus
8
2732 (
4K X 8
) EPROMs.
-
The EPROM will also require the generation of a wait state.
-
The EPROM has an access time of
450ns
.
-
The 74LS138 requires
12ns
to decode.
-
The 8088 runs at 5MHz and only allows
460ns
for memory to access data.
-
A wait state adds
200ns
of additional time.
-
The 8088 cold starts execution at
FFFF0H
. JMP to F8000H occurs here.
-
The
16
62256s on the previous slide are actually SRAMs.
-
Access times are on order of
10ns
.
-
Flash memory can also be interfaced to the 8088 (see text).
-
However, the write time (
400ms
!) is too slow to be used as RAM (as shown in the text).
-
Parity Checking:
-
Parity checking is used to detect single bit errors in the memory.
-
The current trend is away from parity checking.
-
Parity checking adds
1
bit for every
8
data bits.
-
For
EVEN
parity, the
9th
bit is set to yield an even number of 1's in all 9 bits.
-
For
ODD
parity, the
9th
bit is set to make this number odd.
-
For 72-pin SIMMs, the number of data bits is 32 + 4 = 36 (
4
parity bits).
-
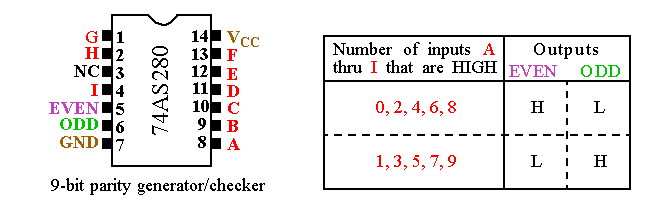
74AS280 Parity Generator/Checker
-
This circuit generates
EVEN
or
ODD
parity for the 9-bit number placed on its inputs.
-
Typically, for generation, the 9th input bit is set to 0.
-
This circuit also checks
EVEN
or
ODD
parity for the 9-bit number.
-
In this case, the
9th
input bit is connected to the
9th
bit of memory.
-
For example, if the original byte has an even # of 1's (with
9th
bit at GND), the parity bit is set to 1 (from the
EVEN
output).
-
If the
EVEN
output goes high during the check, then an error occurred.
-
This parity scheme can only detect a single bit error.
-
Block-Check Character (
BCC
) or Checksum.
-
Can detect
multiple bit
errors.
-
This is simply the
two's complement sum
(the negative of the sum) of the sequence of bytes.
-
No error occurred if adding the data values and the checksum produces a 0.
-
For example:
-
This is not fool proof.
-
If 45 changes to 44
AND
04 changes to 05, the error is missed.
-
Cyclic Redundancy Check (
CRC
).
-
Commonly used to check data transfers in hardware such as harddrives.
-
Treats data as a stream of serial data
n-bits
long.
-
The bits are treated as coefficients of a
characteristic polynomial
,
M(X)
of the form:
-
Cyclic Redundancy Check (
CRC
) (cont.)
-
The
CRC
is found by applying the following equation.
-
G(X)
is the called the
generator polynomial
and has special properties.
-
A commonly used polynomial is:
-
The remainder
R(X)
is
appended
to the data block.
-
When the
CRC
and
R(X)
is computed by the receiver,
R(X)
should be zero.
-
Since
G(X)
is of power 16, the remainder,
R(X)
, cannot be of order higher than 15.
-
Therefore, no more than
2
bytes are needed independent of the data block size.
-
Cyclic Redundancy Check (
CRC
)(cont.)
-
Parity
,
BCC
and
CRC
are only mechanisms for error detection.
-
The system is halted if an error is found in memory.
-
Error
correction
is starting to show up in new systems.
-
SDRAM
has ECC (Error Correction Code).
-
Correction will allow the system can continue operating.
-
If
two
errors occur, they can be
detected
but not
corrected
.
-
Error correction will of course cost more in terms of extra bits.
-
Error correction is based on
Hamming Codes
.
-
There is lots of theory here but our focus will be on implementation.
-
The objective is to correct any single bit errors in an 8-bit data byte.
-
In other words, we need
4
parity bits to correct single bit errors.
-
Note that the parity bits are at bit positions that are
powers of 2
.
-
Hamming Codes (cont).
-
P1 is generated by computing the parity of X
3
, X
5
, X
7
, X
9
, X
11
, X
13
, X
15
.
-
These numbers have a 1 in bit position 1 of the subscript in binary.
-
The 74LS636 corrects errors by storing
5
parity bits with each byte of data.
-
8
data I/O pins
-
5
check bit I/O pins
-
2
control pins
-
2
error outputs
-
Single error flag (
SEF
)
-
Double error flag (
DEF
).
-
See the text for an example of its use in a circuit.