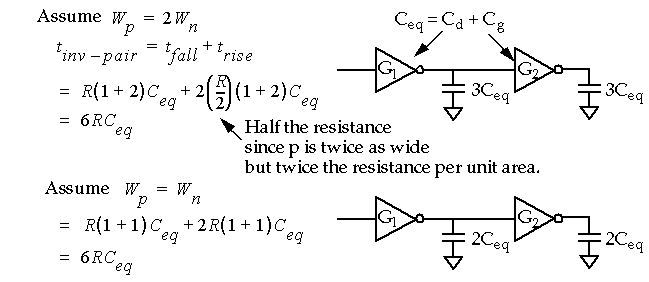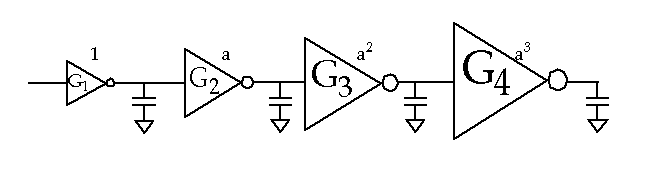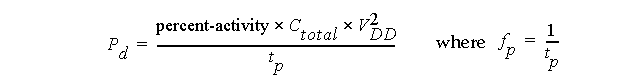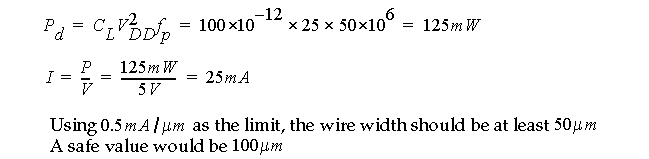Transistor Sizing

• So far, we have assumed that to get symmetric rise and fall times:

• Does this rule reduce overall delay ?

• Therefore, in self-loaded circuits (circuits without significant routing capacitance and fanouts), equal sized devices can be used to reduce power dissipation and area without sacrificing performance (overall delay).

Stage Ratio

• How do we drive large load capacitances, e.g. off-chip wires via the I/O pads, long buses, etc. ?

 

• By using a chain of inverters, where each successive inverter is larger than the previous one.

• What is the optimal value of a (the stage ratio) that both
• Minimizes the delay through the chain.
• Minimizes the area and power.

 

• The magic number a is e (~2.7) - see analysis in book.
• The optimal value may vary depending on process parameters.

Power Dissipation

• Two components of power dissipation in CMOS circuits:
• Static power
• Dynamic power

 

• Static power dissipation:
• Reverse-bias leakage current through parasitic diodes formed by source/drain diffusion and n-well diffusion.
• Through-current of pseudo-nMOS devices.
• Subthreshold conduction (current that flows when V _in < V _tn ).
• Becoming more important as power supply is scaled down.

Static Dissipation

• Reverse-bias leakage current

 

• Total Static Power dissipation:

Dynamic Dissipation

• The current required to charge/discharge capacitive load usually dominates the crowbar (short circuit) current.

 

• For example:

Capacitive Dissipation

• However, slow rise and fall times will increase crowbar current of driven gates.

 

• Assuming a step input and a repetition frequency of f _p , the average dynamic power, P _d , is expressed as:

 

• Therefore power is proportional to
• The switching frequency
• The capacitive load.
• But goes up as V _DD ² .

 

• Also, power is independent of device parameters, such as V _t or beta.

Total Power Dissipation

• P _total = P _s + P _d + P _{short-circuit} (see text P. 236)

 

• Detailed analysis of power is often impractical.

 

• Consider the following simplifications:
• Calculate total capacitance driven by the gates in the circuit.
• Estimate the percentage of the devices operating at the max clock frequency (e.g. 50%).
• Use the dynamic power dissipation expression:

 

• Power minimization:
• Use complementary logic gates to reduce through current (static)
• Use minimum-size devices to reduce diffusion leakage (static).
• Reduce V _DD , the frequency and the switched capacitance (dynamic).

Sizing Routing Conductors

• The size of metal conductors is important because:
• Metal migration.
• Power supply noise and integrity.
• RC delay (considered previously).

 

• Electro-migration is the transport of metal ions through a conductor induced by direct current.

 

• A 'safe' value of current density, J , is:
• 
 

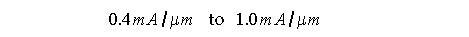
• For example, consider a clock buffer that drives a 100 pF load at 50 MHz:

Sizing Routing Conductors

• Power supply noise and integrity:
• IR drops on V _DD and V _SS (voltage drops due to current spikes and the resistance of the metal) can occur causing gates to fail.

 

• What is the voltage drop (ground bounce) in the power and ground wires if the buffer is 500 microns from the power and ground pads ?

Design Margining

• Sources of variations that effect nominal circuit behavior (2 environmental, 1 manufacturing):
• Operating Temperature
• Supply Voltage: Data sheets give +/- 10%, e.g., 3.0 to 3.6 for 3.3V.
• Process Variation: Normal to keep parts within 2 or 3 sigma.

 

• We must design the circuit to operate over all extremes of these variables.

 

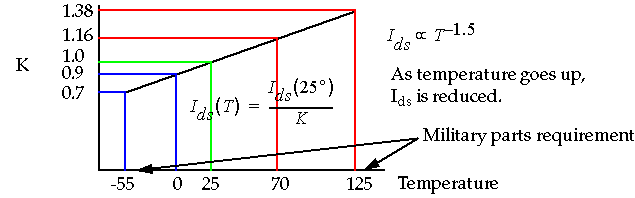
• Temperature :
• What happens to I _ds with temperature ?

Design Corners

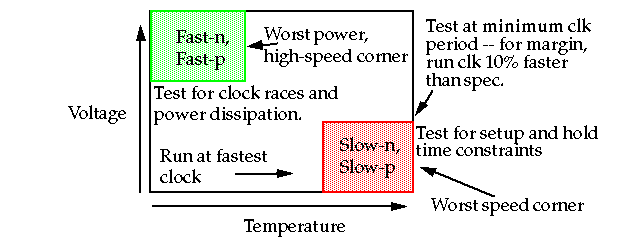
• Sources of process variation include changes in doping densities, oxide thickness and line width variations.

 

• The following boundary combinations may result
• Fast-n, Fast-p
• Fast-n, Slow-p
• Slow-n, Fast-p
• Slow-n, Slow-p

Yield

• Defined as:

• Yield verses Testing

 

• Yield is influenced by:
• Technology
• Chip Area
• Layout

Yield

• A simple model for yield (Seed's model):

 

• Clearly, yield decreases dramatically as the area of the chip increases.

 

• Yield and testing are related by

 

• Another exponential function that states that if yield is low, we better have high test coverage (+99%) otherwise we ship lots of bad parts.

 

• Device testing is a course of its own - stayed tuned.

First Order Approximations of Scaling

• Constant field scaling : 1/alpha scaling applied to all dimensions, device voltages and concentration densities.
• I _ds per transistor scales by 1/alpha.
• # of transistors per unit area scales by alpha ² .
• Current density scales by alpha, power density remains constant (VI/A),
• e.g., (1/alpha*1/alpha)*alpha ²

 

• Constant voltage scaling : V _DD is held constant while process is scaled.
• I _ds per transistor scales by alpha.
• # of transistors per unit area scales up by alpha ² .
• Current density scales by alpha ³ , power density scales by alpha ³ .

 

• Lateral scaling : Only the gate length is scaled ( gate-shrink ).
• I _ds per transistor scales by alpha.
• # of transistors per unit area scales by alpha.
• Current density scales by alpha ² , power density scales by alpha ² .