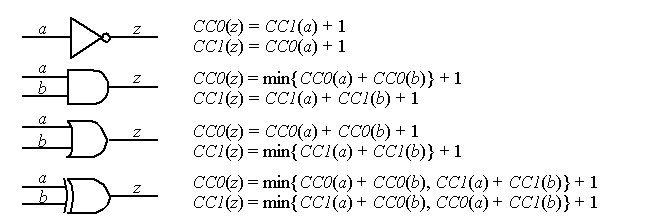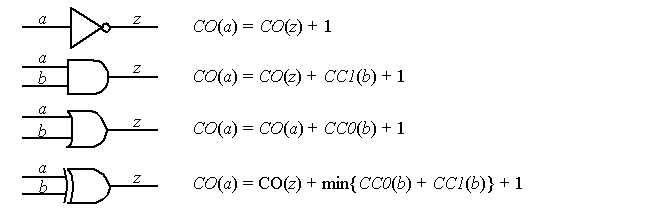-
An attempt to
quantify
testability by Goldstein '79 and Grason '79 resulted in two testability measures,
controllability
and
observability
.
-
Controllability
is defined as the difficulty of setting a particular logic signal to a 0 or a 1.
-
PIs are free (usually assigned a value of 1).
-
Output 1 values for AND gates are more expensive than OR gates.
-
Observability defined as the difficulty of observing the state of a logic signal.
-
Purpose:
-
Analysis of difficulty of testing internal circuit nodes.
-
May need to modify circuit, add observation points or test hardware.
-
Can be used to guide ATPG algorithms, i.e., to help them make decisions by providing information about the difficulty of setting lines.
-
Can be used to estimate fault coverage.
-
Can be used to estimate test vector length.
-
Testability analysis attributes:
-
Requires topological analysis (but no test vectors).
-
It is linear in complexity.
-
Otherwise it's pointless, i.e., might as well use ATPG to compute exact fault coverage.
-
Goldstein developed SCOAP testability measures and describes a linear complexity algorithm to compute them.
-
The algorithm has significant inaccuracies because it assumes that signals at reconvergent fanout stems are independent.
-
B fans out to 3 gates, the outputs of these gates reconverge at the OR gate.
-
The assumption of signal independence is the key behind SCOAP's linear time algorithm.
-
However, this reduces its accuracy in predicting which individual faults will remain undetected and which will be detected.
-
SCOAP testability measures:
-
Controllability: From 1 (easiest) to infinity (hardest).
-
Observability: From 0 (easiest) to infinity (hardest).
-
Combinational measures are related to the number of signals that may be manipulated to control or observe l.
-
Sequential measures are related to the number of times a FF must be clocked to control or observe a line.
-
Another approach is to make them probability based, i.e., they range between 0 and 1.
-
Here, the 1-controllability, C1, is the probability of a signal value on line l being set to 1 by a random vector.
-
W.r.t. fault detection probability, we can cast the problem as the C1 of a signal line that is the XOR of the good and faulty circuit outputs.
-
Problem: Almost doubles the size of the circuit to be analyzed.
-
Alternatively, it can be cast (incorrectly) as the probability of detecting a SA0 fault on line l by a random input, e.g.,
C1(l) * OB(l).
-
Problem: control and observability of a line are NOT independent.
-
Jain and Agrawal address this problem in PREDICT using conditional probabilities for observability.
-
PREDICT computes exact probabilities but has exponential complexity for some circuits.
-
Goldstein's algorithm: SCOAP
-
Consists of 6 numerical measures for each signal (l) in the circuit:
-
Combin. 0-controllability, CC0(l); Sequential 0-controllability, SC0(l)
-
Combin. 1-controllability, CC1(l); Sequential 1-controllability, SC1(l)
-
Combin. observability, CO(l); Sequential observability, SO(l)
-
Controllabilities:The basic process: Set PIs to 1, progress from PIs to POs, add 1 to account for logic depth.
-
In general, if only one input sets gate's output:
-
output controllability = min(input controllabilites) + 1
-
If all inputs set gate output:
-
output controllability = sum(input controllabilities) + 1
-
If gate output is determined by multiple input sets, e.g., XOR:
-
output controllability = min(controllabilities of input sets) + 1
-
Remember that reconverging signals may correlate and therefore this procedure becomes inaccurate at the reconvergence point.
-
Observabilities: The basic process: After controllabilities computed, set P0s to 0, progress from PO to PIs, add 1 to account for logic depth.
-
For example, the difficulty of observing a designated input to a gate is the sum of (1) the output observability (2) the difficulty of setting all other inputs to non-dominant values (3) plus 1 for logic depth.
-
The accuracy problem occurs for the computation of the observability of a fanout stem with n branches.
-
One attempt is to bound the stem probability by:
-
min(all fanout branch observabilities)
-
The events of observing a signal through each branch are independent.
-
max(all fanout branch observabilities)
-
They are all dependent, therefore branch that's hardest to observe is correct choice.
-
Problem: These ignore the possibility that observing a signal may require its propagation through some or all fanout branches.
-
Goldstein uses:
CO(stem) = min(CO(branches))
-
Therefore, observability calculation errors occur and ATPG algorithms which use them may be misled.
-
Goldstein's algorithm has only O(2*n) or O(n) complexity.
-
Note that the red numbers are given by the SCOAP algorithm and the green number are the exact values.
-
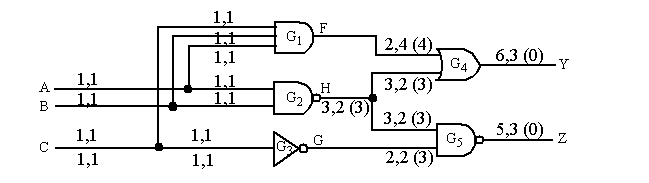
An example with multiple outputs:
-
Let's refer to the branches using the gate index, e.g., A1, A2 and H4, H5, etc.
-
For nodes
F
,
H
and
G
:
-
CC0
(F) = min{
CC0
(A),
CC0
(B),
CC0
(C)} + 1 = 2
-
CC1
(F) =
CC1
(A) +
CC1
(B) +
CC1
(C) + 1 = 4
-
CC0
(H) =
CC1
(A) +
CC1
(B) + 1 = 3
-
CC1
(H) = min{
CC0
(A),
CC0
(B)} + 1 = 2
-
CC0
(G) =
CC1
(C) + 1 = 2
-
CC1
(G) =
CC0
(C) + 1 = 2
-
CC0
(Y) =
CC0
(F) +
CC0
(H) + 1 = 6
-
CC1
(Y) = min{
CC1
(F),
CC1
(H)} + 1 = 3
-
CC0
(Z) =
CC1
(H) +
CC1
(G) + 1 = 5
-
CC1
(Z) = min{
CC0
(H),
CC0
(G)} + 1 =3
-
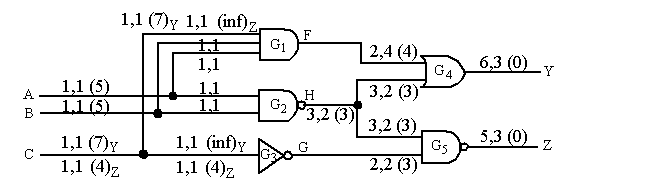
In order to observe node F on PO Y, it is necessary to control H to 0.
-
CO
Y
(F) =
CO
(Y) +
CC0
(H) + 1 = 4
-
CO
Z
(G) =
CO
(Z) +
CC1
(H) + 1 = 3
-
CO
Y
(H) =
CO
(Y) +
CC0
(F) + 1 = 3
-
CO
Z
(H) =
CO
(Z) +
CC1
(G) + 1 = 3
-
Inputs are observable on Y or Z.
-
Consider observability of C via Z:
-
CO
Y
(C) =
CO
Y
(F) +
CC1
(A) +
CC1
(B) + 1 = 7
-
Consider observability of C via Y:
-
CO
Z
(C) =
CO
Z
(G) + 1 = 4
-
Note that C1 is not observable, (inf), on Z and C3 is not observable on Y.
-
Also, SA1 faults on A1 and B1 are not observable because of the redundancy but they are still assigned finite values (left as an exercise).
-
Sequential circuit with scannable FFs (treat as combinational):
-
Eliminate FFs and assign pseudo-primary inputs/outputs, PPIx and PPOx.
-
Levelize the circuit, as shown by the circled numbers in the circuit, for the forward pass.
-
See text for observabilities and more details.
-
Sequential SCOAP measures differences:
-
Increment the sequential measure by 1 only when:
-
Signals propagate from FF inputs to Q or Q, or
-
Signals propagate from FF outputs backwards to D, Clk, SET or RESET inputs.
-
One must iterate on feedback loops until controllabilities stabilize.
-
SC0, SC1 and SO formulas differ from CC0, CC1 and C0 only in that you do NOT add one when moving from one level to another.
-
SC0 and SC1 roughly measure the number of times various FFs must be clocked to control a signal.
-
If line l can only be set to 1 but clocking FF a twice and FF b three times, SC1(l) should be 5.
-
SO correspondingly measure the number of times a FF must be clocked to observe a combinational signal.
-
SCOAP can be used to predict the length of a test set.
-
Testabilities of SA faults at node x given by:
-
T(x SA0) = CC1(x) + CO(x)
-
T(x SA1) = CC0(x) + CO(x)
-
These indicate in order to detect a fault at x, one must set x to the opposite value from the fault and observe x at a PO.
-
A testability index can be computed as:
-
Testability index = log (sum over all faults fi of T(fi)).
-
How are Testability Measures useful?
-
In ATPG during backtracing (controllabilities) and propagating the fault effect (observabilites) since they give the path of least resistance.
-
Some caution is necessary since reconvergent fanout introduce error in controllabilites and fanout stems introduce error in observabilities.
-
How are Testability Measures useful?
-
Tell designer which parts of the design are extremely hard-to-test.
-
Either redesign or special-purpose test hardware is needed to achieve high fault coverage.
-
Extremely useful for estimating fault coverage and test vector length.
-
Fault coverage estimation via testability can reduce CPU time by orders of magnitude over fault simulation (and has only a 3-5% error).